论文链接：[https://www.usenix.org/conference/osdi22/presentation/zheng-lianmin]

内容简介

Alpa通过生成统一数据、操作符和管道并行性的执行计划，自动化大型深度学习(DL)模型的模型并行训练。现有的模型并行训练系统要么要求用户手动创建并行化计划，要么从有限的模型并行配置空间中自动生成并行化计划。它们不足以在分布式计算设备上扩展复杂的深度学习模型。Alpa通过将并行性视为两个层次:操作符间并行性和操作符内并行性来分配大型DL模型的训练。在此基础上，Alpa为大规模模型并行执行计划构建了一个新的分层空间。Alpa设计了许多编译通道，以便在每个并行级别自动派生有效的并行执行计划。Alpa实现了一个高效的运行时来协调分布式计算设备上的两级并行执行。我们的评估表明，Alpa生成的并行化计划可以匹配或优于手动调整的模型并行训练系统，甚至在它们设计的模型上也是如此。与专门的系统不同，Alpa还泛化到具有异构体系结构的模型和没有手动设计计划的模型。

  1. 通过inter-op pass将计算图分割为子图，设备集群分割为device mesh，并寻找将子图分配给device mesh的最佳方式。
  2. 通过intra-op pass为inter-op pass找到每个流水线阶段的子图-device mesh的最佳并行方案
  3. 运行时编排 生成静态指令，按照顺序排列计算和通信操作，并启动设备集群上的分布式计算图推理。

出发点

创新点

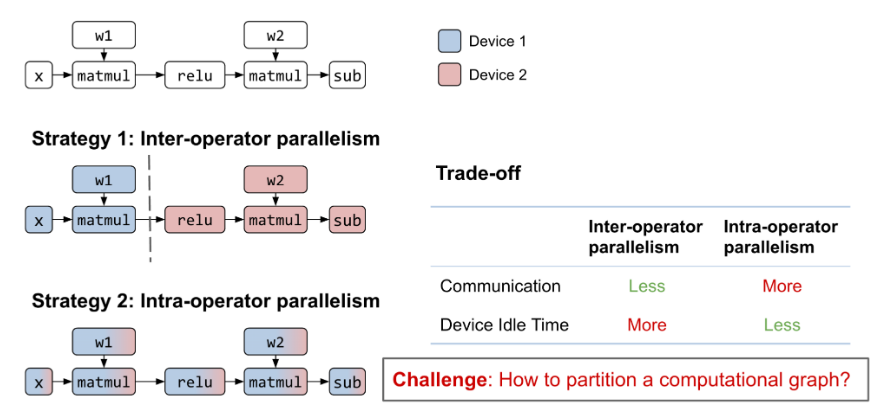
在两个层级上进行分布式并行执行策略：intra-op 和 inter-op ，并且这两种策略可以混合使用。

  • intra-op的并行<个人理解为算子内的并行>，通过整数线性规划(ILP)来最小化执行成本，将其算子内的并行策略分配到分布式设备中的不同网格(mesh)，并返回其最小的执行成本给inter-op并行过程。
  • inter-op的并行<个人理解为算子间的并行>，将模型分割放在分布式设备中的不同网格(mesh)中执行，在该过程中通过DP来最小化不同设备通信的latency成本，最终确定最佳的分布式策略。

以下为这两点的基础示意图

device mesh概念

是将一组物理设备视作2D的逻辑设备。每个设备(x,y)都可以沿着这两个维度以不同的带宽进行通信。假设不同组的设备沿着同一个维度进行通信时具备同样的性能。device mesh可以由节点和GPU灵活组成，例如2个节点，每个节点8个GPU，通过inter-op pass可以将其组成2x8，1x16，4x4，8x2的device mesh，而不会局限于单个节点，这些不同的组合方式会导致不同的设备通信代价<意味着同一个mesh中可能存在跨节点的设备，这就相比与同一个节点设备有更高的通信成本>，后续也会通过inter-op pass 来优化物理设备和逻辑device mesh的映射。

4. Intra-op 并行

在所给的device mesh上，最小化执行计算子图的算子内并行成本。根据工作负载的分配，不同的mesh可能会有不同数量的计算设备。
采用SPMD风格的算子内并行，认为单个device mesh中所有的设备都有等效的计算能力，将所有计算平均分配到所有的设备上，执行相同的指令。 平均分配的方式减少了分布策略的搜索空间，更加方便的表示数据并行，算子并行等策略。这种方式与Tofu和FlexFlow(自动算子并行)不同。与FlexFlow采用的随机搜索和Tofu采用的假设线性不同的是，Alpa采用ILP来求解具有数万个运算符的模型。

算子内并行空间

对于计算图上的一个算子，在mesh上可能有多种并行算法。

对于矩阵乘来说，并行可以在ijk任意维度，或者[跨设备并行化ijk的组合?]，不同的方式就会有不同的计算和通信成本，不同的方式也都要求输入tensor有不同的layout，也导致输出tensor有不同的layout。如果输入的layout和并行方式需求的layout存在差异，那么久需要额外的转换，这也进一步增加通信开销。intra-op pass的目的就是给每个算子选择一个并行策略，来让整个图的执行时间最小。

Sharding Spec

分片规范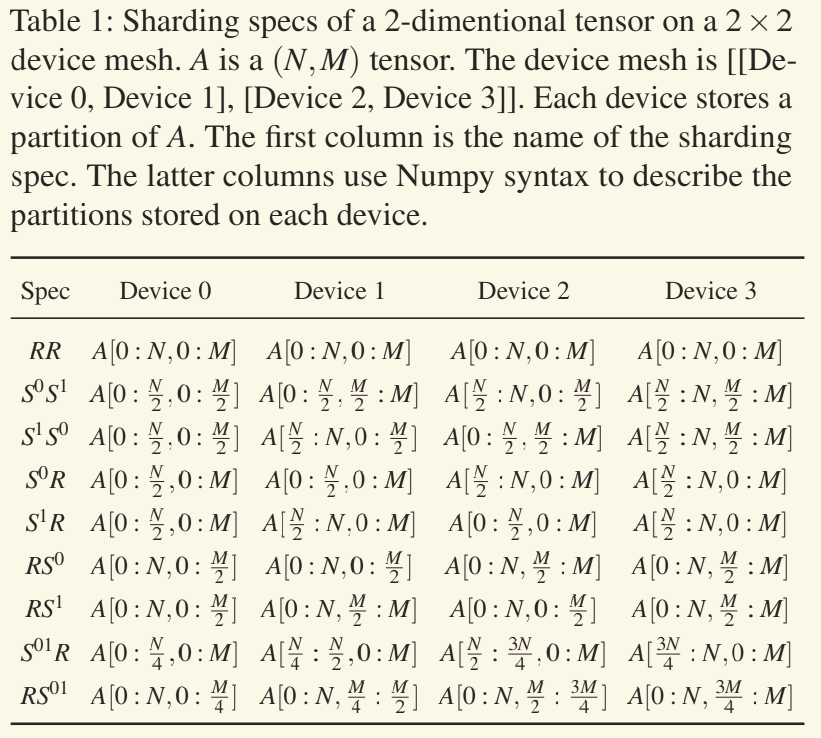

上面这个表格是一组Sharding Spec，用于描述一个tensor的不同layout，对于一个N-D的tensor来说，他的Sharding Spec会被定义为 ， , S表示切分，R表示复制。Table 1.中最左侧就是可选择的layout， 表示在mesh的第一个维度进行切分，表示在mesh的两个维度都进行切分，Spec中的两个字母表示tensor的两个维度的sharding策略。

Resharding


当一个算子的输入tensor layout不满足当前为该算子选择的并行策略，且这个并行策略可能会有跨设备的通信，就需要加入 resharding这个layout转换。表格2. 就是几个resharding的例子。例如，a)要将一个全复制的tensor转换成其他的sharding spec时(case 1) ，可以在不通信的情况下局部切分tensor；b)交换切分轴(case 4)，需要使用all-to-all的通信源语了，详见Communication_primitives。

算子的并行算法

结合以上内容，考虑在2D的mesh上将一个3D矩阵乘 并行化。表3. 列出了几种算子内并行策略

最左侧一列表示将哪个维度进行并行，0和1 表示并行于mesh哪个维度。此外例如conv和reduction也可以通过分析其数学表达式来得到类似的所有可并行策略。Alpa中使用XLA的HLO作为基础算子，(为啥是XLA呢，因为算子少，工作量少 :-) )

ILP 公式

一个计算图全部的执行开销包含：所有算子的计算开销、通信开销以及所有路径的resharding开销。
这里将成本最小化表述为ILP，并通过一个现成的求解其进行最优求解。以下是论文，后续再看。

http://www.decom.ufop.br/haroldo/proglinear/files/cbcUserGuide.pdf

对于一个算子, 可能存在的并行策略数量是 ，有一个通信开销向量 长度为 ，或者可以描述为 <长度为的实数向量空间>，表示第i个策略的通信开销。类似的，计算开销向量表示为 。同时有一个决策向量 来表示那个策略被使用， 表示我们给算子选择了第i个并行策略。对于算子之间的Resharding开销来说，定义了一个矩阵 ，表示算子的第i个并行策略的输出到算子的第个并行策略的输入的Resharding开销
目标函数如下:

前一部分是算子的计算开销和通信开销，后面一部分是从算子到算子 的resharding开销。在上面这个公式中是变量，其余都是常量值。第二部分是二次方程式，所以无法使用ILP求解器。这里通过引入一个新的决策向量将其线性化，这个向量表示算子之间的resharding决策。新的公式如下：

虽然可以通过分析来获得上面三个常量的准确成本，但是为了简单起见，采用了以下方法来评估它们。

  1. 用通信字节数并除以mesh维度带宽来得到通信开销、
  2. 将所有的计算开销设置为0，动机与https://arxiv.org/abs/1807.08887 一致，
    • 具体原因需要阅读该论文

之所以进行这样的简化是因为：

  1. 对于计算量很高的算子，例如matmul，不允许在重复计算。所有的并行策略总是会把所有的工作都分配到所有的设备上，所以一个算子所有的并行策略都会具有相同的算数复杂度。
  2. 对于计算量不高的算子，例如element-wise，允许复制操作，但是它们的计算开销可以忽略不计。
    为了简化计算图，将计算量极少的算子进行融合，比如element-wise、transpose、reduction等，将这些算子融合到计算图的其他算子中，并将目标算子的sharding spec进行传播，从而使这些计算量很少的算子尽可能的隐藏到其他算子庞大的计算开销、通信开销中。这种方式极大的减少了计算图中算子的数量，从而减少了ILP问题的大小。通过广度优先遍历的方式来计算每个算子的深度，然后将这些计算量少的算子尽可能的融合到最深的算子里。
    一旦并行策略被ILP决定，就会应用一系列post-ILP通信优化，就比如在合适的情况下将all-reduce操作用reduce-scatter和all-gather取代，因为后者减少了复制tensor的数量和相应的计算量，同时保持通信量不变，这也达到了与权重sharding或者ZrRO优化其一样的效果。

5. Inter-op 并行

在最小化算子间并行的延迟问题上，主要考虑如何切分模型和device cluster到每个阶段和mesh，以及如何将他们映射成stage-mesh对。优化的目标是最小化整个计算图端到端pipeline的执行延迟，[17，33] 论文中已经考虑了一些简单的问题，例如假设每个阶段的设备是预先分配好的，并且所有阶段都是有固定的数据或者算子并行策略。Apla中通过联合考虑device mesh的分配和每个阶段存在不同的算子内并行策略舍弃了这些假设。

算子间并行策略的搜索空间

假设计算图中包含了一个算子序列，并且具备图一样的拓扑顺序，标记为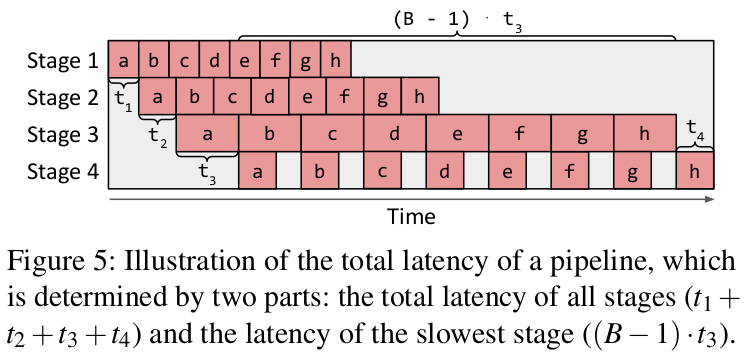 ，其中操作的输入来自。将其切分为S个阶段 ，每个阶段都有一些算子组成 ,并且将每个阶段分配到一个大小的的子mesh上，子mesh是从包含deivce的计算机集群中切分出来的，这个计算机集群标记为带有形状为的cluster mesh。让 作为执行 阶段在大小为的子mesh上执行的延迟，这是通过ILP得出的最小延迟，由intra-op pass中返回给inter-op pass。

Curio：上图中abcd..表示一个输入的不同batch，stage表示子图和device mesh的组合，时间表示每个stage执行一个batch的时间开销。总体的延迟就是最耗时的子图的所有batch的计算时间加上一个batch的其他子图的执行时间(其他batch的其他子图执行的时间就被掩盖到最耗时的子图执行时间中，这部分的计算中主要是取决于子图-device mesh的划分，尽可能将数据依赖和子图的执行时间开销平衡)

如图所示，假设有B个不同的输入微batch，对于整个计算图的最小延迟可以表示为如下公式。

Missing or unrecognized delimiter for \left T^{*} = \min_{\substack{s_1,…,s_S \ (n_1,m_1),…,(n_S,m_S)}} \left { \sum^S_{i=1} t_i + (B-1) \cdot \max_{1\leq j\leq S}{t_j} \right } \tag{2}

总延迟包含两个部分：第一部分是所有阶段的总延迟，解释为第一个微batch通过整个流程的延迟；第二部分是剩余个微batch的执行时间，该时间由最慢的阶段所限制，如上图中的第三阶段。
目标是解决上述带有两个约束的公式：1）对于计算图前向传播的算子，我们想要将其与对应的反向算子放在同一个子mesh上。因为反向传播通常使用一系列与正向传播相似的tensor，这有效地减少从前向传播中获取所需的tensor到反向传播阶段的通信量。使用前向和后向的延迟之和作为 ，所以公式2反映了总体的延迟，包括了前向和后向。2）需要已经切分的子mesh能够完全地覆盖的集群mesh——不浪费任何计算设备资源。接下来详细说明DP公式。

DP 公式

为了确保所有的子mesh能够完整的覆盖的mesh集群，将可用的子mesh的形状转化为两种类型：
1）1D的子mesh，形状为 ；
2）2D的子mesh，形状为，这种方式充分地利用了mesh集群的第二个维度（例如，在一个GPU集群中，这意味着每一个物理机器充分使用所有的计算设备）；
具体的定理证明见附录A，表明了这些特定的子mesh能够始终完全覆盖mesh集群。
为了将集群中的物理设备分配给DP算子找到的结果子mesh，分配设备时按照从大尺寸mesh到小尺寸的策略，即优先为较大的子mesh分配设备，然后再分配给小的子mesh。

<这样的分配逻辑有助于充分利用高性能的通信链路，因为在大型子网格中，设备间的通信往往更为高效。这是因为大型子网格可能横跨多台物理机器，而这些机器之间的数据传输速度通常高于单台机器内部设备间的传输速度。？？？？源自LLM的解释>

当有多个相同大小子mesh的pipeline阶段时，倾向于将相邻的pipeline阶段放的更近，从而减少通信延迟。

–==剪枝的策略==–
对于一系列子mesh， 的组合配剔除集合中，这些组合有着较差的表现，因为作为可选的子mesh具有更多可以用高带宽进行通信的设备，这种简化中只需要确保

为了求解公式2的 ，这里开发了一个动态规划算法。
首先枚举了第二项 并且对于每个不同的最小化第一项 ，具体来说，当将算子使用函数 来表示把从第个算子到最后的算子序列切分为个阶段后，分配到个设备上的最小总延迟，任何一个阶段的延迟都不超过 。开始时设置 ，推导出F的最优子结构为：

$$
F(s,k,d; t_{\max}) = \min_{\substack{k \leq i \leq K \ n_s \cdot m_s \leq d}}
\begin{cases}
t_{\text{intra}}((o_k, …, o_i), \text{Mesh}(n_s, m_s), s) \

  • F(s-1, i+1, d-n_s \cdot m_s; t_{\max}) \
    | t_{\text{intra}}((o_k, …, o_i), \text{Mesh}(n_s, m_s), s) \leq t_{\max}
    \end{cases} \tag{3}
    $$

并推导出最佳总延迟为:

其中是由intra-op pass来决定的，这是子序列阶段在上执行子图的最低延迟。这个Mesh是一系列物理设备，因此枚举出所有逻辑mesh潜在的shape可能性，并通过intra-op pass查询子图、当前mesh和子图的输入的来自其他intra-op 的设置，并得到一个intra-op的计划。
之后按照这个计划和其他的一些low-level编译器优化(fusion,mem)来编译这个子图，得到一个可执行文件来进行精确的分析。这个可执行程序是为了获取这个stage的延迟和每个设备上执行这个阶段所需要的mem，以及保存中间结果所需要的mem。之后根据所选择的pipeline执行计划来检查这个需要的mem是否与设备的mem合适，这里存在一个约束：

也就是说执行这个stage需要的内存加上保存中间结果的内存必须小于设备内存(显而易见的约束，不然多出来的放到设备外？增加通信代价，得不偿失)，选择一个满足最小延迟同时满足设备mem的逻辑mesh，如果都不满足，就把置0。
这个DP算法是基于TeraPipe的，然而TeraPipe中假设所有pipeline stage都是相同的，并且目标是找到一个最优的方式将带Batch的输入token组织成大小不同的微batch。alpa的目标是将计算图的算子划分成不同的组，放到不同的pipeline stages，是在假设所有微batch都有相同的大小。此外alpa用DP算法在inter-op pass中优化每个stage pipeline 的mesh shape。

  • TeraPipe论文阅读
复杂度

在 的时间内计算固定的切分。最多有 种选择: 和所有子mesh选择。因此总的复杂度是 。这个时间复杂度对于大的计算图(超过1W个算子)来说并不可行。为了加速DP，做以下实用的优化

early pruning

提前剪枝，
1）递增枚举：方法类似于TeraPipe，将从小到大列举，
2）当大于当前最优的，立刻停止枚举。这是因为较大的无法提供一个更好的解决方案。
3）同样，在枚举的时候，每次只评估比上一个大至少ε的. 虽然找到的解决方案不一定是最优的，但是全局最优条件的差距最大为 。 按照经验设定 ，实验中该算法找到的方案基本上和最优解一致。

运算符聚类

计算图上的很多算子并不是计算密集的，这些算子的确切位置对总体执行的时间影响很小。这里开发了另一个DP算法来聚类相邻的算子，从而减少计算图的大小。将K个算子聚类成L层，L是远小于K的。 这个算法的目的是将两种类型的算子合并：1）不会调用大量的计算，但是会增加计算图的长度；2）相邻的算子如果放在不同的设备上可能会产生实质性的通信。定义函数 作为聚类算子时划分到聚类层r时接收的最大数据量的最小值。最优子结构如下

其中， 表示从到的输入数据总量，表示整个计算图的FLOP。确保每个聚类层的FLOP都是在 1 + δ乘以每层平均FLOP之内的同时，也最小化了个层间FLOP的方差，从而达到更加均匀的结构分布。对于通信成本相同的方案，我们选择结构最均匀的一个，同事最小化每层FLOP的方差。通过这个DP算法，我们可以在的时间内算出最优的层聚类。 是算法的超参数，根据经验我们基于设备数量和计算图中计算量大的算子数量选择一个小的。其实这个选择对于最终性能并不会有跟明显的影响。

算法描述

Inter-op pass总结
输入：计算图G , 集群C {with shape (N,M)}
输出：最小的执行延迟 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 计算图前处理
1. 序列化模型
   (o_1,...,o_k) = Flatten(G)
2. 算子层聚类
   (l_1,...,l_L) = OperatorClustering(o_1,...,o_K)
# 执行intra-op pass，获取不同stage-mesh组合
submesh_shapes = {(1,1),(1,2),(1,4),...,(1,M)}∪{(2,M),(3,M),...,(N,M)}
for 1<=i<=j<=L :
	stage = (l_i,...l_L)
	for (n,m) in submesh_shapes:
		# 初始化所有intra-op阶段的
		for s in range(1,L):
			t_intra(stage, Mesh(n, m), s) = INF
		for (n_l,m_l),opt in LogicalMeshShapeAndIntraOpOptions(n,m):
			plan = IntraOpPass(stage, Mesh(n_l,m_l),opt)
			t_l,mem_stage,mem_act = Profile(plan)
			for s 满足公式5 # mem_stage + s · mem_act ≤ mem_device .
				if t_l <= t_intra(stage, Mesh(n, m), s):
					t_intra(stage, Mesh(n, m), s) = t_l
return t_l

# inter-op pass （DP）
T* = INF
for t_max in SortedAndFilter(t_intra, ε):
	if B·t_max >= T*:
		break
	F(0,L+1,0; t_max) = 0
	for s in range(1,L):
		for l in range(L,1):
			for d in range (1,N*M):
				Compute F(s,l,d; t_max) 按照公式3
	T*(t_max) = min_s{F(s,0,N·M;t_max)}+(B−1)·t_max
	if T*(t_max) < T*:
		T* = T*(t_max)
return T*

6. Parallelism Orchestration并行编排

当Stages，device mesh的分配决定以后，在intra-op pass阶段，Alpa遵循ILP求解器得出的intra-op并行计划，根据分配给它的device mesh编译每个阶段。编译依赖于XLA和GSPMD，并生成每个stage-mesh的并行可执行程序。当需要时，编译会自动插入第四节中提到的通信源语来处理算子内并行所需要的resharding。
在inter-op pass阶段，Alpa实现了一个额外的并行编排pass来处理跨mesh的stage间通信，并为算子间并行执行生成静态指令。

跨mesh的Resharding


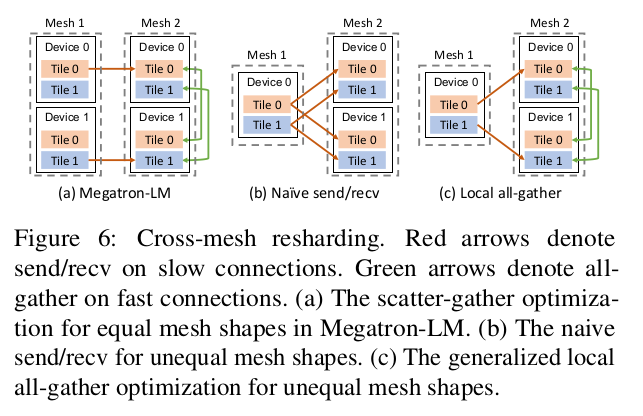
现存的手动系统，就像Megatron-LM，约束所有的pipeline stage都有相同的数据和tensor模型并行度，因此pipeline stage之间的通信通常通过两个等效设备网格的对应设备之间的P2P发送/接收来实现(图6a)。在Alpa中包含两个相邻stage的device mesh可能有不同的mesh shape，并且tensor在两个stage之间的通信可能有着不同的sharding spec(图6b/c)，这里称这种通信模式为cross-mesh resharding，这是一个多对多的多点传送问题。
给定tensor在发送和接收方的mesh上的sharding spec， Alpa在两次迭代中生成一个用于解决 corss-mesh sharding 的通信方案。第一次迭代中，计算在源mesh和目标mesh之间tensor tile的对应关系。基于此，生成源设备和目标设备之间的P2P发送/接收源语来实现通信。然后，第二次迭代中来识别目标tensor在其sharding spec中存在复制的机会。在这种情况下tensor只需要在mesh之间传输一次，之后利用目标mesh上利用更高的带宽通过 all-gather来完成交换–这会重写第一次迭代中生成的发送/接收，避免重复通信。
称这种方法为 local all-gather跨设备resharding。因为在Alpa的设计中stage之间的通信通常都很小，实验符合设计的期望，后续还会开发更优的跨设备resharding策略。

生成可执行指令

最后一步，Alpa生成静态执行指令在集群上启动训练，因为每个stage都有不同的算子集合，并且在放在有不同shape 的mesh上 （与很多APMD 并行训练系统不同），Alpa采用MPMD风格的runtime来安排算子间并行执行–Alpa生成确定的静态执行指令给每一个device mesh。
Alpa给算子间并行执行开发了一系列指令，包括stage内tensor的内存分配和释放指令，按照cross-mesh resharding方案在stage间的tensor通信指令，同步指令和计算指令等。。。根据用户选择的pipeline schedule，Alpa使用一个驱动进程提前生成指令，并在执行之前整个指令列表分发给每个worker，避免了运行时的驱动和worker之间协调的开销。

7. 限制和讨论

相比于现有的一些手动组合数据、算子、和pipeline并行(比如3D-parallelism [45]和PTD-P[40])，Alpa对inter-op、intra-op并行性的分层视图显著的提高了他们的三个主要灵活性：1）stage可以包含不均匀数量的算子和层；2）stages可能被映射到不同shape的device mesh上；3）在每个stage中，数据和算子并行结构配置对于每个算子来说都是单独定制的。综上，是的Alpa能够整合所有现存的模型并行方法并推广到具有更多异构性的模型结构和集群设置。
抛开这些改进，Alpa的优化算法目前还是存在一些限制：

  • 并没有对不同stage的通信成本进行建模，因为cross-stage的通信成本本来就很小。但是实际上在DP或者ILP中对cost进行建模都是可行的，但是会需要枚举更多矢量的intra-op pass和DP状态。
  • inter-op pass目前有一个超参数：微batch ，目前的公式中并没有被优化，但是可以通过枚举的方式进行搜索。
  • inter-op pass用静态线性schedule建模pipeline的并行结构，而没有考虑更多动态schedule，例如在不同的deivce上并行计算图中的不同分支
  • 对于overlap计算和通信并没有优化一个最好的方案，Alpa值能处理静态计算图，所有tensor的shape编译时已知。
    尽管如此，Alpa都是可以将现在一些常见的模型生成出接近最优的执行方案。

附录

关于算子聚类的疑惑解释

在Alpa论文中的动态规划（DP）公式里，递推关系中取两部分的最大值的原因是为了确保负载均衡和计算效率。这种方法有助于找到一个平衡点，使得每个阶段（或者子任务）的最大开销最小化，从而实现整体优化。

公式回顾

公式如下：

解释

  • ( G(k, r) )：表示将前 (k) 个算子分成 (r) 个阶段时的最小成本。
  • 递推关系：

为什么要取最大值

  • 最大值的含义：在每个划分点 (i)，我们计算两部分的最大值：
    1. G(i-1, r-1) ：前 (i-1) 个算子分成 (r-1) 个阶段的最小成本。
    2. ( C(i, k) )：从第 (i) 个算子到第 (k) 个算子的聚类成本。
  • 最大值的目的是为了确保最坏情况下的开销最小化：
    • 在分布式计算中，如果某一个阶段的计算开销特别大，它将成为整个系统的瓶颈，导致整体性能下降。
    • 通过取两部分中的最大值，公式确保即使在最坏情况下（即某一阶段的开销最大），整体方案依然是最优的。这种策略有效地平衡了各个阶段的负载，避免单点过载。

为什么要取最小值

  • 最小值的含义：在所有可能的划分点 (i) 中，选择使得最大值最小的那个划分点。
  • 最小值的目的是找到全局最优解：
    • 动态规划通过递推关系逐步寻找全局最优解。在每一步中，选择最优的划分点，以确保整体开销最小。
    • 通过在所有可能的 (i) 中取最小值，公式确保选择的划分点能够使整体计算开销最小化。

负载均衡与效率优化

  1. 负载均衡：

    • 分布式系统中，负载均衡至关重要。均衡的负载分布可以避免某些设备过载，从而提高整体系统的效率。
    • 通过限制每个阶段的FLOP数，并取最大值来衡量最坏情况下的开销，公式确保每个设备的计算任务不会超过其承受能力。

  2. 效率优化：

    • 通过动态规划逐步优化，从而找到整体计算开销最小的方案。
    • 在每一步中选择使得当前阶段最优的划分点，确保最终得到的划分方案是全局最优的。

总结

在Alpa论文中的DP公式里，取两部分的最大值是为了确保分布式计算的负载均衡和效率优化。这种方法通过考虑最坏情况下的开销，避免了单点过载，从而提升了整体系统的性能和稳定性。最终通过在所有可能的划分点中取最小值，公式实现了全局最优的算子聚类和任务分配方案。

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。